
《应用数学》


说出来你可能不信,量子物理学并不是一个很难理解的学科。就像所有的物理理论一样,它最终只是由一系列规则和数学公式组成。量子物理学与日常经验物理学唯一的区别是,这些规则可能看起来是违反直觉的、不寻常的。这篇文章不是要教你详细的量子物理,而是要让你相信它可以被理解。
首先,我们讨论测量量子系统的状态。
在经典物理学中,我们想当然地认为我们可以完全了解一个物理系统的状态。只要有可能制造出一种足够精确的尺子、温度计和秤,那么就有可能以任意高的精度知道一个系统的长度、温度或质量。我们也理所当然地认为,系统的状态是独立于我们的测量工作而存在的。如果我们测量一个房间的尺寸,我们理所当然地认为即使我们停止测量,这个房间的尺寸仍然会保持不变,如果房间的尺寸发生变化,那么这种变化将是一个可知的物理过程的结果(房子的热膨胀等),此外,即使我们不测量房间的长度和宽度,我们也理所当然地认为,在任何时候,它的长度和宽度都只有一个值。
当我们开始研究量子物理时,我们必须抛弃这些关于世界的假设。这不仅仅是因为量子系统的精确测量在实践中是不可能的,还因为量子系统状态的“精确测量”在物理上不再有意义。量子系统存在于态的叠加中,系统在同一时间处于所有可能的状态,但是每个状态都有一个概率振幅,当你测量系统时,在那个特定状态下观察系统的可能性有多大。
其中一个最好的例子就是著名的施特恩-格拉赫实验实验。
这个实验是奥托·斯特恩和沃尔特·格拉赫在1922年做的。一束中性银原子通过一个不均匀的磁场,并观察到银原子束分成两束,其中一束向磁场方向偏转,另一个偏转方向与磁场相反。
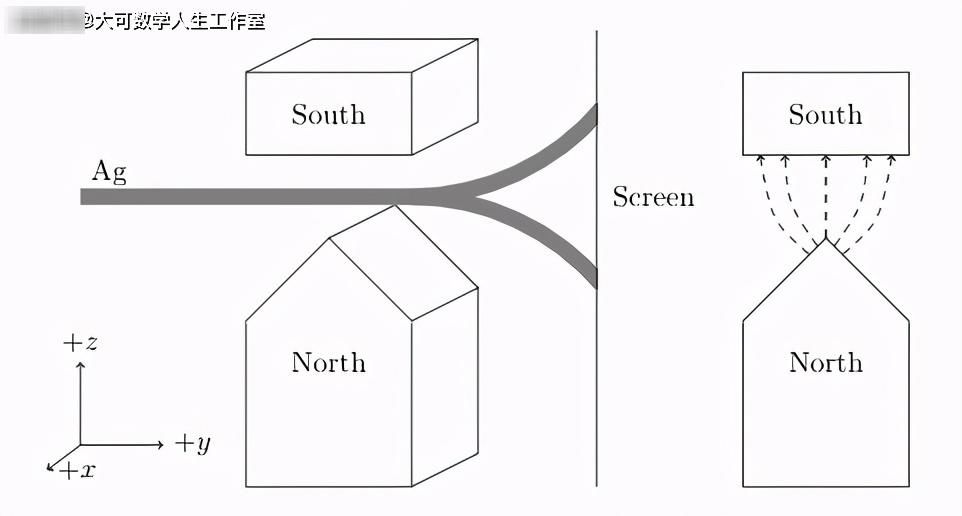
有些原子偏转与磁场完全平行,有些偏转与磁场完全反平行,如果每个原子是一个纯磁偶极子,磁矩是μ,这就是我们所期望的行为。银原子与磁场相互作用的势能则为U=-μ·B,使作用在粒子上的力为F=?(μ·B)。磁场在x和y方向上非常接近均匀,所以力在z方向上它的大小是:
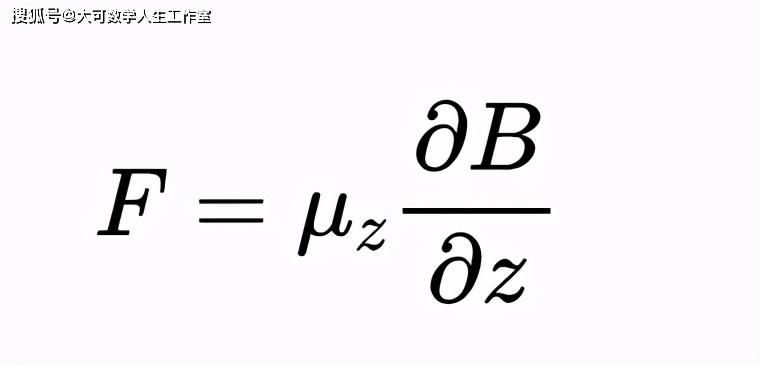
式中,μz为原子磁矩在z方向上的分量。对于绕圆周运动的带电粒子(如电子绕原子核运动),我们从经典电磁理论中知道,磁矩有两个贡献者,第一个是与带电粒子围绕力的中心(在这种情况下是原子核)的轨道角动量相关的项:
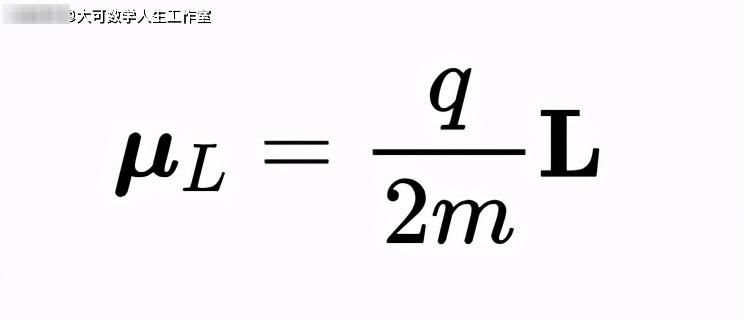
第二个是与固有角动量相关的项,即带电粒子绕自身轴的自旋:
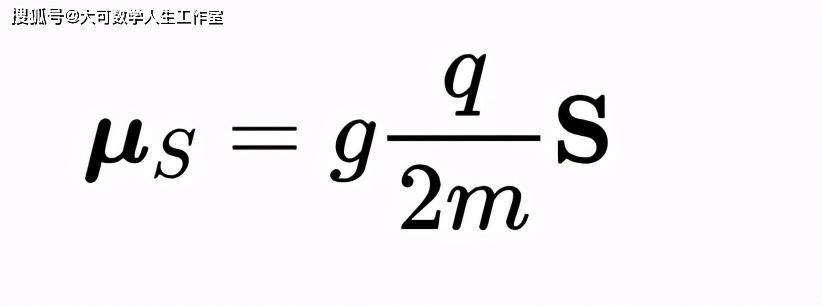
在第二个公式中,g是一个称为旋磁比的无因次量,其值约为2.0023。计算它是非常困难的,所以我们就不计算了。在讨论原子中的电子时,我们知道,电子既不像行星绕着太阳那样绕着原子核转,也不像小陀螺那样绕着自己的轴旋转。它们只是为了实现原子的磁相互作用,在某种意义上,如果这是真的,原子的磁矩就是我们所期望的。
选择银原子进行实验并非偶然。银的电子构型是:
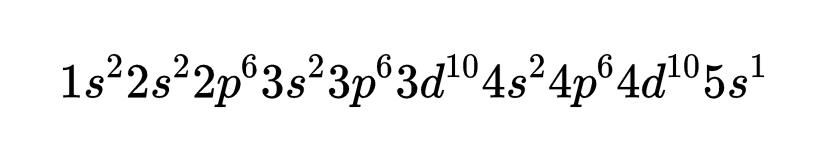
原子的前46个电子都在闭合壳层中,而闭合壳层没有净角动量。此外,泡利不相容原理告诉我们,闭合壳层中的电子自旋将被抵消。这意味着,唯一能对磁矩有贡献的电子,是5s轨道上的单个电子。由于s轨道没有轨道角动量,影响银原子总磁矩的唯一因素是5s轨道上单个电子的自旋。
传统意义上,我们认为原子的磁矩是随机分布的,而银束通过磁场的结果是会在屏幕上形成一个“喷溅”,反映出原子的随机方向和大小。但相反,银束被清晰地一分为二。
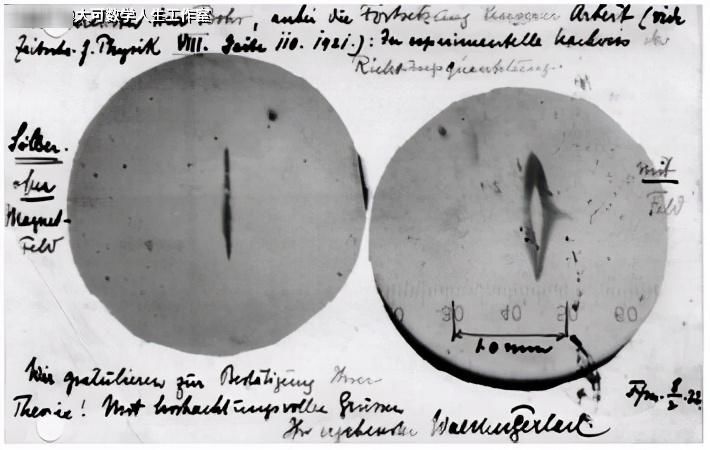
上图是1922年进行的原始实验的幻灯片。银原子穿过仪器,在载玻片上形成一层银。左边的幻灯片是磁场开启前的照片。之所以没有两个完美的点,是因为银束是通过一个狭窄的矩形狭缝进行准直的,现代实验已经纠正了这一点。尽管如此,分裂(只有0.2毫米)是清晰可见的,而且在分裂的中心可以清楚地看到两束不同的银束击中了幻灯片。这表明电子的自旋只能取两个可能的值,这两个值经实验确定为:
上一篇:2022考研数学余丙森【概率论与数理统计】强化课
下一篇:没有了