分数的意义和性质

（九）教材第60、61页

1.填空。

（1）2的因数有（1，2)，8的因数有（1,2,4,8），2和8的最大公因数是（2)。

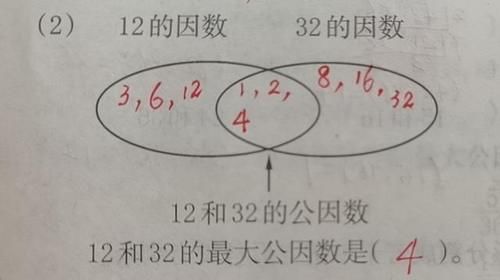
(2)12的因数

32的因数

12和32的公因数

12和32的最大公因数是(4)。

2.先用“√”标出第一列各个数的因数，再填空。

12和16的最大公因数是(4)。

12和20的最大公因数是(4)。

16和20的最大公因数是(4)。

12，16和20的最大公因数是(4)。

3.已知A不等于B，且A和B都不等于0。

(1)A是B的倍数，A和B的最大公因数是(B)。

(2)B是A的倍数，A和B的最大公因数是(A）。

（3）A和B都是质数，A和B的最大公因数是(1）。

(4）A和B是连续自然数，A和B的最大公因数是(1）。

4.写出下列各分数中分母和分子的最大公因数。

12/36（12）

12/18(6)

6/7（1）

1/18（1）

42/63（21）

54/36(18)

（十）教材第62页

1.写出下列各组数的最大公因数。

28和70

28和70的最大公因数（14）

16和92

16和92的最大公因数（4）

42和56

42和56的最大公因数（14）

72和36

72和36的最大公因数（36）

11和33

11和33的最大公因数（11）

65和39

65和39的最大公因数（13）

15和16

15和16的最大公因数（1）

24和36

24和36的最大公因数（12）

2.把一个长48cm、宽36cm的长方形分割成若干个正方形且没有剩余。

（1)正方形的边长分别是(1，2，3，4，6，12)，共有(6)种不同的分法。

（2）最少可分割成（12）个正方形。

(3)最多可分割成(1728)个正方形。

3.五(1）班有40人，五(2）班有35人。如果每班分成人数相等的小组进行跳长绳比赛，那么每个小组最多有多少人?

40和35的最大公因数是5

答：每个小组最多有5人。

4.学校操场长100m，宽60m。现计划在操场四周种树，要求每两棵树的间距相等，四个角上各种一棵树。共有几种符合要求的种法？每隔多少种一棵树比较合理?

可以每隔1m，2m，4m，5m，10m，20m6种符合要求的种法。

根据树的大小和实际密度要求，每隔10m一棵树或其他方式合理种植。

*5.把3根长度分别为12cm，16cm，24cm的木条，分割成相同长度的若干段(正好分完，没有剩余)，然后制作等边三角形。最多可以制作多少个等边三角形?

（12+16+24）÷3=17…… 1

答：最多可以制作17个等边三角形。